β-test version 0.1.3, July 31, 2009.
Introduction
starPad
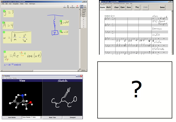 We envision an
aggregation of applications that use post-WIMP, pen-centric interfaces to make
computational assistance more natural and efficient; among such applications
are MathPad2 and MathPaper,
the Music Notepad, and ChemPad, shown in the image. We originally called that theoretical
aggregation *Pad, using ‘*’ as a wildcard, but are now calling it
starPad for easier location through search engines.
We envision an
aggregation of applications that use post-WIMP, pen-centric interfaces to make
computational assistance more natural and efficient; among such applications
are MathPad2 and MathPaper,
the Music Notepad, and ChemPad, shown in the image. We originally called that theoretical
aggregation *Pad, using ‘*’ as a wildcard, but are now calling it
starPad for easier location through search engines.
The starPad SDK
The goal of the starPad SDK project is to make
it easier for people to write these sorts of applications by providing a
convenient interface for a broad layer of pen-centric functionality in addition
to some research functionality. Currently, it is written for MS Windows .Net
and uses WPF. It includes a convenient interface to stroke-level operations, a
recognition library for handwritten math and gestures, some UI techniques such
as GestureBar, and a pen- and gesture-based application shell supporting
selection, undo, zooming, text input, images, and save/load.
Copyright and License
Except where noted, all source code in this distribution is
Copyright © 2009 Timothy Miller, Robert Zeleznik, Andrew Bragdon, and Chuanjun
Li with contributions by Alex Weiss, Travis Fischer, Joseph J. LaViola Jr.,
Andrew Forsberg, Andrew Brindamour, Gal Peleg, Ali Ozler, Michael Feldman, and
Greg Pascale. The Unicode data files are copyrighted and licensed as noted in
the files. The DollarRecognizer code is based on that provided by Wobbrock,
Wilson, and Li. The math fonts used are the (beta test) STIX fonts, copyrighted and licensed as
noted in the fonts themselves (though you may need a font editing program or
the Microsoft
OpenType Font Properties Extension installed to see the license proper).
Our interface to Mathematica uses version 1.2 of Mathematica's
netlink library,
slightly modified to give access to multiple-precision values.
Their license
only allows non-commercial distribution of the netlink library, but
it would be simple to convert our code to use the stock library without multiple-precision
value support.
For the code owned by us, the license in the two paragraphs following
this one applies. We are essentially making the code free for non-commercial
use. The authors disagree as to whether to make the code free for commercial
use as well and have agreed to postpone the decision until and unless someone
actually wants to use it for such a purpose. So, if you want to use our code in
a commercial product, please get in touch with us: {tsm,bcz,acb}@cs.brown.edu.
Permission to use, copy, modify,
and distribute this software and its documentation for any purpose other than
its incorporation into a commercial product is hereby granted without fee,
provided that the above copyright notice appear in all copies and that both
that copyright notice and this permission notice appear in supporting
documentation, and that the names of Brown University or the authors or the
contributors not be used in advertising or publicity pertaining to distribution
of the software without specific, written prior permission.
BROWN UNIVERSITY, THE AUTHORS,
AND THE CONTRIBUTORS DISCLAIM ALL WARRANTIES WITH REGARD TO THIS SOFTWARE,
INCLUDING ALL IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR ANY PARTICULAR
PURPOSE. IN NO EVENT SHALL BROWN UNIVERSITY, THE AUTHORS, OR THE CONTRIBUTORS
BE LIABLE FOR ANY SPECIAL, INDIRECT OR CONSEQUENTIAL DAMAGES OR ANY DAMAGES
WHATSOEVER RESULTING FROM LOSS OF USE, DATA OR PROFITS, WHETHER IN AN ACTION OF
CONTRACT, NEGLIGENCE OR OTHER TORTIOUS ACTION, ARISING OUT OF OR IN CONNECTION
WITH THE USE OR PERFORMANCE OF THIS SOFTWARE.
Compilation Prerequisites
You will need:
- Visual Studio 2008 SP1 or better. You do need at least SP1,
or you will get mysterious errors regarding Microsoft.Ink.
- The Windows SDK
for Windows Vista or later. You may be able to substitute the Tablet PC SDK
stuff in the list below if you know what you’re doing, but the Windows SDK
seems to be the official/preferred distribution.
- F# (May 2009 CTP, or, hopefully, later).
You may still need (these were previously required but may
be included in the Windows SDK):
Compilation
The main demonstration program is called AnApp, and is
located in Apps\AnApp\AnApp.sln. The startup
project should be set to AnApp. (Frequently this is set wrong by VS when people
first open the solution in a clean source tree, for unknown reasons.)
In the Libs\Math directory tree there
are a couple of test scaffold applications for various pieces of the math system
which also generally serve as usage examples, particularly MathRecoScaffold.
The Source Tree
General code notes:
- You should assume that nothing in the code we're distributing is
thread safe.
- All namespaces in the library code begin with “
starPadSDK.”,
which is generally omitted here.
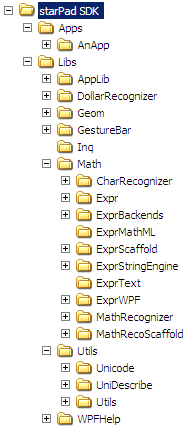 The tree is divided into two main pieces: Apps and Libs. Apps holds applications intended for end users which also
provide usage examples demonstrating the functionality of the SDK. Libs holds the generally useful library of modules the
SDK provides, along with some utilities.
The tree is divided into two main pieces: Apps and Libs. Apps holds applications intended for end users which also
provide usage examples demonstrating the functionality of the SDK. Libs holds the generally useful library of modules the
SDK provides, along with some utilities.
Apps
Currently, the only general example application is . AnApp is intended to be a fairly solidly
designed program expecting to have to handle a range of application
functionality, including undo/redo, the GestureBar for providing accessibility
to gestures (visible as the toolbar-like strip across the top of the main
window), and complicated event handling. It also supports entry and computation
with handwritten mathematics.
Libs
in the Libs directory implements much of the reusable application-level
functionality of Apps\AnApp. This includes a
variety of gestural commands (Commands.cs), a
system to tie them together (CommandSet.cs),
undo/redo (Undo.cs), a selection mechanism (Floatie, Selection*.cs), a
generic inking canvas that can display strokes interleaved with FrameworkElements
(general WPF UI elements) (InqScene.cs), and a mode
for interacting with math (MathEditor.cs).
contains
an implementation of a simple but effective and trainable “$1” gesture
recognizer published in UIST 2007 by Wobbrock, et al. in “Gestures without libraries,
toolkits or training: a $1 recognizer for user interface prototypes”.
contains various
typed point, vector, etc. structs and related other things like lines, angle
units, etc., as well as some simple geometric utilities such as convex hull.
The point, vector, etc. structs provide a more complete set of operations and
operator overloads than Microsoft’s analogous structs, and are also designed so
that all operations have a pure functional form available. They can be viewed as
a complete replacement for Microsoft's WPF point types because of bidirectional
implicit conversions. By providing typed
angle structs such as Rad and Deg,
we allow automatic conversion between them, simplifying some code. They also
allow, for instance, functions to construct rotation matrices to take radians
as an argument while allowing programmers to write either Rotate(Math.Pi/2)
or Rotate(90.Deg()) or Rotate((Deg)90)
to get the same result. We provide extension methods on built-in numeric types
to support things such as 90.Deg() if you are using starPadSDK.Geom. (Intellisense does not provide a menu
of completions after you type something like “90.”, but
invoking the List Members command will bring it up.) We also provide line and
line segment structs with various operations on them.
implements the
work described in “GestureBar: Improving the Approachability of Gesture-based Interfaces”,
by Andrew Bragdon, et al., published at CHI 2009. It provides an approachable
UI for learning gestural interactions that enables a walk-up-and-use experience
which is in the same class as standard menu and toolbar interfaces. Leveraging
the familiar, clean look and feel of a common toolbar, GestureBar on demand
reveals targeted, rich gesture disclosure information consisting of animated
images, detail tips and an out-of-document practice area. GestureBar's simple
design is also general enough for use with any recognition technique and for
integration with standard, non-gestural UI components. The GestureBar has its
own introductory document in Libs\GestureBar\How to Add a
Gesture to GestureBar.
is our equivalent of the WPF classes related to Stroke,
but using our geometry classes (points, etc) and providing some extra convenience accessors
such as Perl-style indexing (use stroq[-1] to get the
last point in the stroq, for instance). The most basic class to know is Stroq,
our equivalent of the WPF Stroke class.
There's also InqCanvas,
the equivalent of InkCanvas, which you can use to
collect and display Stroqs without having to deal with Strokes.
StroqCollection is similarly
analogous to StrokeCollection. StroqElement
allows the display of just one Stroq as a WPF element. If
you have “using starPadSDK.Inq.MSInkCompat;” in your
usings section, you can get the functions that are in the
pre-WPF strokes but not in WPF (cusps, self-intersections, etc.). Gesturizer.cs provides the basic infrastructure
underneath AppLib’s handling of gestures. Features.cs
has a number of tests for various features that might be part of gesture definitions.
Inq.BobsCusps has a cusp-finding algorithm available as
FeaturePointDetector.FeaturePoints() and used by our math recognition code.
contains a set of
related modules for recognizing, representing, computing on, rendering, and
exporting mathematics. These are described at the end of this section.
contains a
class that allows you to reference any Unicode character by name and get the
name of any Unicode character provided by value. This is used primarily by the Math code, but is usable by other applications as well.
is a
Visual Studio plugin (not compiled or tested in a while) which adds a context
menu item to the text editor to show you the Unicode name of the character in
the current selection. It’s also primarily for working with the Math code.
provides a
bunch of utilities that have nothing intrinsically to do with starPad, except that
we wanted to use them, and they seem like things that ought to belong in a
library (or should have been in the C# library), often modeled after the C++
standard library and/or Common Lisp. It also provides a facility for batching
together multiple operations on the same object before, for instance,
triggering a callback; this is used internally by a couple of libraries.
currently contains
WPFutil.cs, which was intended to have utilities
for WPF such as finding bounding boxes of FrameworkElements,
and currently also has a number of other files for dealing with Win32 interoperability
for use in the screen capture functionality of AnApp.
Libs\Math
For description beyond that here of the mechanisms
used and the UI techniques (mostly) available, see these papers:
- Robert Zeleznik, Timothy Miller, and Chuanjun Li. Designing UI Techniques for
Handwritten Mathematics. In EUROGRAPHICS Workshop on Sketch-Based Interfaces
and Modeling, p. 91–98, August 2007.
- Robert Zeleznik, Timothy Miller, Chuanjun Li, and Joseph J. LaViola
Jr. MathPaper: Mathematical
Sketching with Fluid Support for Online Computation. In Smart Graphics:
9th International Symposium, SG 2008. Rennes, France, August 2008. Lecture
Notes in Computer Science 5166, p. 20–32. Springer-Verlag: Berlin,
Heidelberg.
- Chuanjun Li, Robert Zeleznik, Timothy Miller, and Joseph J.
LaViola Jr. Online
Recognition of Handwritten Mathematical Expressions with Support for Matrices.
Proceedings of the 19th International Conference on Pattern Recognition.
December 2008.
The math code can be divided roughly into two parts:
recognition, and everything else:
Recognition
The recognition code is composed of two packages: , which does character recognition,
and , which parses the spatial
structure of the recognized characters into math semantics. The primary user
entry point for the math recognition system is the class MathRecognizer.MathRecognition;
this takes care of doing character recognition too. The mathematical semantics
output of the recognition code is represented in a class structure we called Expr before we came across three or so other mathematical
representation class structures also called Expr; see
below. See the MathRecoScaffold test program for simple examples of use of the
recognizer, computation, and rendering subsystems; AnApp also makes use of the
math code.
Implementation notes: This is a partial port of code
from our MathPaper system, which used Windows Forms; MathRecognition
is partly a glue class which converts from Stroqs and
WPF Strokes to Windows Forms Strokes.
The glue is not a perfect shield, so some UI techniques require knowing about
Windows Forms Strokes and translation to and from them
(handled by the StroqInkMapper Sim member of a MathRecognition object). Not all of the UI techniques from
MathPaper have been ported to the starPad SDK yet, but the translation is
generally fairly simple given the old code.
Everything else
The project contains
the Expr class system for representing mathematical
semantics (Expr.cs), and a system for exporting LaTeX
(TeX.cs). The semantics of Exprs is only
defined for relatively standard functions (+, −, sin, etc.) and then only by
comments in the WKSID enum.
Effectively, other functions are defined by their translations in the various
export and computation systems. Additionally, Syntax.cs contains
(see Syntax.Fixes)
definitions of operators used in parsing stroke input and in formatting results
for WPF, LaTeX, and MathML.
The project
contains code for interfacing with computational backends to computer on Exprs. Currently we have our own quick BuiltInEngine
(incomplete and somewhat buggy) as well as interfaces to Mathematica (most
tested) and Maple (new, not tested much). There is also an interface to a StringEngine (see ExprStringEngine
below).
To call a math backend engine, first you need to find it in
the list of enabled engines in Engine.Engines. (Note
that Mathematica, and potentially other engines, can have multiple versions
available within the same engine.) See the ExprScaffold test program for some
example code on making a menu of all the engines and selecting the right one
when a menu item is selected. (This code is now in MathRecoScaffold as well.) Window1.Window1() builds the menu, and Window1.ChangeEngine()
sets the current engine--the actual setting is done in the line that sets Engine.Current and possibly the Variant
field on the engine, if it has multiple versions.
To evaluate an expression (without substituting variables
defined outside of the expression), you call Engine.Simplify()
or Engine.Approximate(). Simplify
preserves the exact value, so sqrt(2) will come out as sqrt(2), while
approximate is like Mathematica’s N[] function that
approximates the answer by numerically evaluating everything with
floating-point numbers. (These correspond respectively to the arrow and
double-arrow in MathPaper and MathRecoScaffold.) Those functions are called in
ExprScaffold’s Window1.__exprEntry_KeyDown(), but the
calls are basically trivial.
Right now, you have to call Engine.Substitute()
for each variable substitution you want to happen, including substitutions of
variables into other variable definitions. For an example of this, look in the MathRecoScaffold
solution in Evaluator.cs at MathRecoScaffold.Evaluator.SubstMathVars(IEnumerable<Parser,ParseResult>,
Expr) (the function is overloaded, so be sure the argument types are
right in the one you look at). You can ignore the call to SubstSubscript
unless you want to substitute variables in subscripts, which is not normally
done unless you're using them for array indices. Actually, looking at this SubstMathVars I'm not sure it's written the way it ought to
be (it was ported from older code), but it should work, and at least
demonstrates Substitute().
The project
contains code for exporting to and importing from Presentation MathML. It’s
written in F# for easier pattern recognition in parsing MathML. Unfortunately,
it seems that MathML is too loose a standard for certain expressions to have an
easily findable single representation which is parsed by all the input engines
we’ve tested, so there are options available depending on what the expected
receiver of the generated MathML is. NB: if any project you reference
from an application uses this project, you should add the Expr project to the application’s
references in order to get the MathML dtd directory
from the Expr project copied to the directory the program is built in. That
directory is in the Expr project because F# projects appear not to allow adding
directories and files and setting them to be copied automatically. NB2:
if you use this project and have a program installer, be sure that it copies
the MathML dtd directory from the Expr project to
the directory the program is installed in.
The
project is part of an interface to a backend engine we’re not (yet?)
distributing. It’s pretty generic, though, designed for any math engine that
takes MathML and returns MathML.
The project contains
a system for importing into Expr from a simple text format and exporting two
simple text formats (one is very simple, while the other is closer to how
a human might enter the math). Note that this is primarily for debugging;
round-trip integrity is not guaranteed, for instance. For entry points, see the
static public methods available on starPadSDK.MathExpr.Text
(Text.fsi and Text.fs).
This project is also written in F# so that it can use F#’s parser- and
lexer-generators, via hand-made edits to the project file.
The project draws
a typeset form of the input Expr into a WPF
DrawingContext, based on the algorithms described in
The TeXbook. See MathRecoScaffold for examples of use;
MathExpr.ExprWPF.EWPF.Draw*(…) are the
primary entry points, but EWPF.Compose() is used for
special purposes (see the implementations of the Draw*()
methods). It relies on the fonts in the STIXfonts
folder of the project. NB: if any project you reference from an
application uses this project, you should add the ExprWPF project to the application’s
references in order to get the STIXfonts directory
copied to the directory the program is built in. NB2: the STIXfonts folder must be copied to the application
installation directory in any installer for a program that uses ExprWPF. If not otherwise noted, cryptic comments in the source mentioning appendices or page numbers refer to those in The TeXbook.
 We envision an
aggregation of applications that use post-WIMP, pen-centric interfaces to make
computational assistance more natural and efficient; among such applications
are MathPad2 and MathPaper,
the Music Notepad, and ChemPad, shown in the image. We originally called that theoretical
aggregation *Pad, using ‘*’ as a wildcard, but are now calling it
starPad for easier location through search engines.
We envision an
aggregation of applications that use post-WIMP, pen-centric interfaces to make
computational assistance more natural and efficient; among such applications
are MathPad2 and MathPaper,
the Music Notepad, and ChemPad, shown in the image. We originally called that theoretical
aggregation *Pad, using ‘*’ as a wildcard, but are now calling it
starPad for easier location through search engines. The tree is divided into two main pieces:
The tree is divided into two main pieces: